Graphs
Graph Data Structure and Algorithms
Definitions
-
Graph - A set of vertices connected pairwise by edges.
- A vertex is a point on a graph where multiple edges meet
- There has to be a vertice on either end of the edge
- Loop - An edge that starts and ends at same vertex

- Path - A sequence of vertices connected by edges. Two vertices are called connected if there is a path between them.
- Cycle - A path that starts and ends at the same vertex.
Types of graphs
- Undirected graphs are graphs whose edges don’t have direction, and can to both ways
- Directed graphs are graphs whose edges have a direction
Ex. social media (who follows who; directed), road networks (which roads connect to which other roads; undirected), etc.
- Unweighted graphs are graphs whose edges have no value attached to them. Weighted graphs are graphs whose edges have a value. The value on each edge is called its weight.
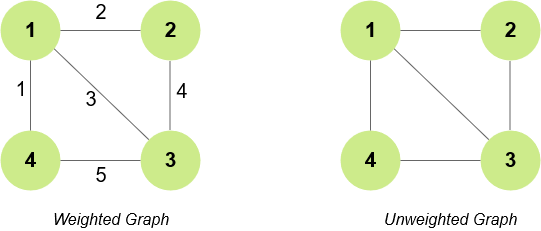
Ex. cost of a flight ticket, distance between two cities, etc.
// from https://algs4.cs.princeton.edu/13stacks/Bag.java.html
import java.util.Iterator;
import java.util.NoSuchElementException;
public class Bag<Item> implements Iterable<Item> {
private Node<Item> first;
private int n;
private static class Node<Item> {
private Item item;
private Node<Item> next;
}
public Bag() {
first = null;
n = 0;
}
public boolean isEmpty() {
return first == null;
}
public int size() {
return n;
}
public void add(Item item) {
Node<Item> oldfirst = first;
first = new Node<Item>();
first.item = item;
first.next = oldfirst;
n++;
}
public Iterator<Item> iterator() {
return new LinkedIterator(first);
}
private class LinkedIterator implements Iterator<Item> {
private Node<Item> current;
public LinkedIterator(Node<Item> first) {
current = first;
}
public boolean hasNext() {
return current != null;
}
public Item next() {
if (!hasNext()) throw new NoSuchElementException();
Item item = current.item;
current = current.next;
return item;
}
}
}
Graph
This is the class containing the necessary properties and methods to implement a graph.
How can you represent a graph using code? Instead of purely trying to visualize it, it's easier to think of what a graph is at its core: a collection of vertices and edges. Furthermore, an edge can be defined by the 2 vertices that it connects.
There are a few ways to represent a graph. We will be using the adjacency list representation. First, we create a simple list of length V, where V is the number of vertices in the graph. This list represents all of the vertices in the graph: the index of 0 represents vertex 0, for example.
How do we account for edges? The way we do this in this representation is that each index of the list of vertices contains a bag of integers. This bag contains all of the vertices that the vertex at that index is connected to.
import java.util.NoSuchElementException;
public class Graph {
private static final String NEWLINE = System.getProperty("line.separator");
// The total number of vertices
private final int V;
// The total number of edges
private int E;
// declaring an array of bags
private Bag<Integer>[] adj;
// Graph constructor must include number of vertices
public Graph(int V) {
if (V < 0) throw new IllegalArgumentException("Number of vertices must be non-negative");
this.V = V;
// must add all edges after the vertices are initialized
this.E = 0;
// casting is required here. We initialize the array of bags.
adj = (Bag<Integer>[]) new Bag[V];
// next, we initialize the bag at each index of the array
for (int v = 0; v < V; v++) {
adj[v] = new Bag<Integer>();
}
}
// get # of vertices
public int V() {
return V;
}
// get # of edges
public int E() {
return E;
}
// error checking method
private void validateVertex(int v) {
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
}
// method to add an edge.
// To define an edge we need two vertices.
// To implement it, we need to make sure v and w both know they are connected.
// Index v of the adjacency list represents vertex v. The bag at this index contains
// all of the vertices that index v shares an edge with. Therefore, we just have to add
// vertex w to this bag. We must also do the same for vertex w; meaning, we add v to
// the bag at vertex w
public void addEdge(int v, int w) {
validateVertex(v);
validateVertex(w);
E++;
adj[v].add(w);
adj[w].add(v);
}
public Iterable<Integer> adj(int v) {
validateVertex(v);
return adj[v];
}
public int degree(int v) {
validateVertex(v);
return adj[v].size();
}
public String toString() {
StringBuilder s = new StringBuilder();
s.append(V + " vertices, " + E + " edges " + NEWLINE);
for (int v = 0; v < V; v++) {
s.append(v + ": ");
for (int w : adj[v]) {
s.append(w + " ");
}
s.append(NEWLINE);
}
return s.toString();
}
public static void main(String[] args) {
// Example of how to initialize a graph.
Graph G = new Graph(7);
G.addEdge(0, 1);
G.addEdge(0, 2);
G.addEdge(0, 6);
G.addEdge(0, 5);
G.addEdge(6, 4);
G.addEdge(4, 3);
G.addEdge(4, 5);
G.addEdge(3, 5);
System.out.println(G);
}
}
Graph.main(null);
Note that the output from the above tester method initializes the graph pictured above the class.
Searching a Graph
There are two common algorithms for searching a graph: Depth First Search and Breadth First Search.
We will use the term "exploration" of a vertex to mean visiting all of its adjacent vertices.
BFS: Explore a vertex completely before picking the next one. The first vertex you visit doesn't matter, but from there you should only explore vertices that you have already visited. In the below image, we first visit 0. We must fully explore 0, so we then visit 1 and 2 since they are connected to 0. Next, we explore 1 since we visited it first after 0, which means we visit vertices 3 and 4. Since we visited vertex 2 second, we fully explore it now and visit 5 and 6. The order of exploration would then be 3, 4, 5, 6 but of course there are no further adjacent vertices to visit.
DFS: Again, the first vertex you visit doesn't matter. However, we don't explore this vertex. Instead, we keep on visiting adjacent vertices until there are no more vertices to visit. Then, we backtrack until there is another adjacent vertex to visit. Instead of fully exploring any vertex, we go down the tree (depth first). In the below image, we choose 0 to visit first. We arbitrarily then visit vertex 1. Then, we visit vertex 3 since it is adjacent to vertex 1. Since 3 is not adjacent to any other vertices, we go back to vertex 1 and try to find another adjacent vertex; we visit vertex 4. 4 is not adjacent to any other vertices, so we go back to vertex 1. 1 is not adjacent to any other vertices so we go back to vertex 0. Now, we visit 2, then 5. We then go back to 2 and visit 6. Once we backtrack to 0 and find that there are no more adjacent vertices to explore, we are done.
Depth First Search
One method to search all of the vertices and edges in a connected graph. Start at a random vertex and mark it. Then, go to any vertex connected to the starting vertex and mark it. Continue to do this until you have explored all vertices along this path. Then, retrace back one step, and see if you can explore any other vertices. Continue to do this until you get back to the root. Then do the same thing again. It is called depth first search because you fully explore the entire root of a node first, before moving on.
public class DepthFirstSearch {
private boolean[] marked;
private int count;
public DepthFirstSearch(Graph G, int s) {
marked = new boolean[G.V()];
validateVertex(s);
dfs(G, s);
}
private void dfs(Graph G, int v) {
count++;
marked[v] = true;
for (int w : G.adj(v)) {
if (!marked[w]) {
dfs(G, w);
}
}
}
public boolean marked(int v) {
validateVertex(v);
return marked[v];
}
public int count() {
return count;
}
private void validateVertex(int v) {
int V = marked.length;
if (v < 0 || v >= V)
throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V-1));
}
public static void main(String[] args) {
Graph G = new Graph(7);
G.addEdge(0, 1);
G.addEdge(0, 2);
G.addEdge(0, 6);
G.addEdge(0, 5);
G.addEdge(6, 4);
G.addEdge(4, 3);
G.addEdge(4, 5);
G.addEdge(3, 5);
int s = 0;
DepthFirstSearch search = new DepthFirstSearch(G, s);
for (int v = 0; v < G.V(); v++) {
if (search.marked(v))
System.out.print(v + " ");
}
System.out.println();
if (search.count() != G.V()) {
System.out.println("NOT connected");
}
else {
System.out.println("connected");
}
}
}
DepthFirstSearch.main(null);
Another implementation uses Stacks. The idea is that you push the root node onto the stack, and then pop it off. Then, you push all of the nodes connected to the root node onto the stack. Then, you pop the top node off the stack, and push all of the nodes connected to that node onto the stack. Continue to do this until the stack is empty.
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class DFS {
private static final int N = 100000 + 1;
private static List<Integer>[] adj;
private static boolean[] visited;
public static void main(String[] args) {
// Create the adjacency list
adj = new List[N];
for (int i = 0; i < N; i++) {
adj[i] = new ArrayList<>();
}
visited = new boolean[N];
// Add edges to the adjacency list
adj[0].add(1);
adj[0].add(2);
adj[1].add(2);
adj[2].add(0);
adj[2].add(3);
// Start DFS from node 2
dfs(2);
}
private static void dfs(int node) {
System.out.print(node + " ");
visited[node] = true;
for (int next : adj[node]) {
if (!visited[next]) {
dfs(next);
}
}
}
}
DFS.main(null);
BFS can be implemented using Queues. We start at a random vertex and mark it. Then, we add all of the vertices connected to it to the queue. Then, we dequeue the first vertex in the queue and mark it. Then, we add all of the vertices connected to it to the queue. We continue to do this until the queue is empty.
In other words, at each layer we queue all of the nodes, then check all of them before continuing to the next layer.
import java.util.*;
public class BFS {
static final int N = 100000 + 1; // define max nodes
static List<Integer> adjList[] = new ArrayList[N]; // adj list is array of lists
static boolean visited[] = new boolean[N];
static Queue<Integer> q = new LinkedList<>();
static void bfs(int node) {
visited[node] = true;
q.add(node);
while (!q.isEmpty()) {
node = q.poll();
System.out.print(node + " "); // process node
for (int next : adjList[node]) {
if (!visited[next]) {
visited[next] = true;
q.add(next);
}
}
}
}
public static void main(String[] args) {
for (int i = 0; i < N; i++) {
adjList[i] = new ArrayList<>();
}
adjList[0].add(1);
adjList[0].add(2);
adjList[1].add(2);
adjList[2].add(0);
adjList[2].add(3);
bfs(2); // start from node 2
}
}
BFS.main(null);
One popular database that utilizes graphs is called Neo4j. I used this while working at the San Diego Supercomputer Center for various kinds of data that could be represented well using graphs.
Here's an example of how this could be used in relation to something simple like forming CSA groups:
As you can see, we have a great visualization of nodes and edges(relationships) using this. Also, we can store as many properties as we want within each node and edge. Additionally, we can give nodes and edges labels, which we can then query against using the Cypher query language. The simplest cypher query is pictured, where MATCH(n) RETURN n returns all nodes and edges in the database.
Another example is using graphs to represent molecules:
